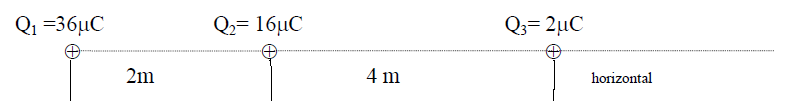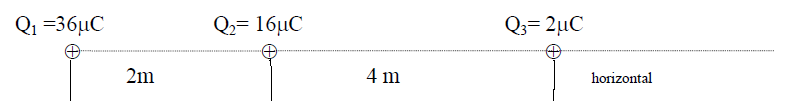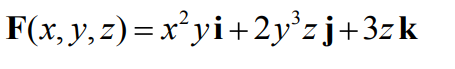ELETROMAGNETISMO
Duas partículas puntiformes estão localizadas num plano cartesiano sobre o eixo, sabendo que a partícula q1 = 4 nC, se localiza em x = 0,200 m e a outra
partícula q2 = +5 nC se localiza em x = - 0,300 m. Determine aproximadamente o módulo da força resultante que essas duas partículas exercem sobre uma terceira
partícula q3 = - 6 nC localizada na origem. Considere a constante eletrostática igual a 9.109 N.m2/C2
2,40 x 10-6 N
14 x 10-6 N
21 x 10-6 N
40 x 10-6 N
7,2 x 10-6 N
Determinar a intensidade da força elétrica em N, entre um próton e um elétron ,sabendo que a distancia entre o próton e o elétron num átomo de hidrogênio é de 5,3.10-¹¹m, considere que a carga do elétron seja igual a carga do próton  C e considere a constante eletrostática igual a
C e considere a constante eletrostática igual a  N.m²/c².
N.m²/c².
8,2.10-8
3.10-¹¹
5.10-5
5,3.10-¹¹
7,3.10-¹4
Calcule o divergente de G(x, y, z) = xzi + xyzj − y2k.
div F = 5z + 3xz.
div F = z + xz.
div F = 4z +2xz.
div F = 3z +7yz.
div F = 5z + xz.
Determine aproximadamente o ângulo ente os vetores w e v
w= (5; 12) e v= ( -15; 8)
600
700
35,50
460
84,50
Para uma distribuição infinita de cargas que produz um campo de 4, 5 × 104 N/C a uma distância de 200 cm. Calcule a densidade de carga linear. Considere a constante eletrostática igual a 9.109 N.m2/c2.
5.10-6 C/m
3.10-9 C/m
7.10-9 C/m
3.10-7 C/m
9.10-9 C/m
Uma partícula de 1,8 nC está no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Qual é aproximadamente o fluxo elétrico em N/C .m2 através da superfície? Considere a permissividade elétrica igual a 8,85 x 10 -12 farad por metro.
92
652
203
402
562
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 5 x 105 N m²/C
ΦE = 4 x 106 N m²/C
A figura abaixo representa três esferas puntiformes fixas, no vácuo.calcule aproximadamente a intensidade da força elétrica resultante sobre a esfera Q2 , considere a constante eletrostática igual a  N.m²/c².
N.m²/c².
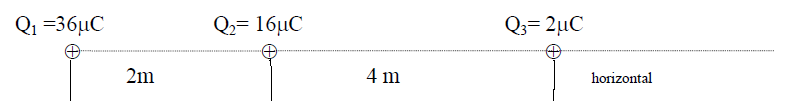
2,40 x 10-6 N
14 x 10-6 N
21 x 10-6 N
40 x 10-6 N
7,2 x 10-6 N
Determinar a intensidade da força elétrica em N, entre um próton e um elétron ,sabendo que a distancia entre o próton e o elétron num átomo de hidrogênio é de 5,3.10-¹¹m, considere que a carga do elétron seja igual a carga do próton  C e considere a constante eletrostática igual a
C e considere a constante eletrostática igual a  N.m²/c².
N.m²/c².
8,2.10-8
3.10-¹¹
5.10-5
5,3.10-¹¹
7,3.10-¹4
Calcule o divergente de G(x, y, z) = xzi + xyzj − y2k.
div F = 5z + 3xz.
div F = z + xz.
div F = 4z +2xz.
div F = 3z +7yz.
div F = 5z + xz.
Determine aproximadamente o ângulo ente os vetores w e v
w= (5; 12) e v= ( -15; 8)
600
700
35,50
460
84,50
Para uma distribuição infinita de cargas que produz um campo de 4, 5 × 104 N/C a uma distância de 200 cm. Calcule a densidade de carga linear. Considere a constante eletrostática igual a 9.109 N.m2/c2.
5.10-6 C/m
3.10-9 C/m
7.10-9 C/m
3.10-7 C/m
9.10-9 C/m
Uma partícula de 1,8 nC está no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Qual é aproximadamente o fluxo elétrico em N/C .m2 através da superfície? Considere a permissividade elétrica igual a 8,85 x 10 -12 farad por metro.
92
652
203
402
562
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 5 x 105 N m²/C
ΦE = 4 x 106 N m²/C
A figura abaixo representa três esferas puntiformes fixas, no vácuo.calcule aproximadamente a intensidade da força elétrica resultante sobre a esfera Q2 , considere a constante eletrostática igual a  N.m²/c².
N.m²/c².
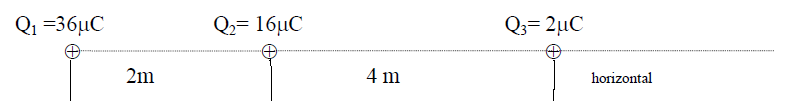
8,2.10-8
3.10-¹¹
5.10-5
5,3.10-¹¹
7,3.10-¹4
Calcule o divergente de G(x, y, z) = xzi + xyzj − y2k.
div F = 5z + 3xz.
div F = z + xz.
div F = 4z +2xz.
div F = 3z +7yz.
div F = 5z + xz.
Determine aproximadamente o ângulo ente os vetores w e v
w= (5; 12) e v= ( -15; 8)
600
700
35,50
460
84,50
Para uma distribuição infinita de cargas que produz um campo de 4, 5 × 104 N/C a uma distância de 200 cm. Calcule a densidade de carga linear. Considere a constante eletrostática igual a 9.109 N.m2/c2.
5.10-6 C/m
3.10-9 C/m
7.10-9 C/m
3.10-7 C/m
9.10-9 C/m
Uma partícula de 1,8 nC está no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Qual é aproximadamente o fluxo elétrico em N/C .m2 através da superfície? Considere a permissividade elétrica igual a 8,85 x 10 -12 farad por metro.
92
652
203
402
562
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 5 x 105 N m²/C
ΦE = 4 x 106 N m²/C
A figura abaixo representa três esferas puntiformes fixas, no vácuo.calcule aproximadamente a intensidade da força elétrica resultante sobre a esfera Q2 , considere a constante eletrostática igual a  N.m²/c².
N.m²/c².
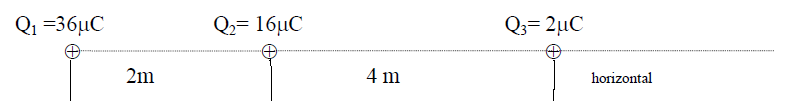
div F = 5z + 3xz.
div F = z + xz.
div F = 4z +2xz.
div F = 3z +7yz.
div F = 5z + xz.
Determine aproximadamente o ângulo ente os vetores w e v
w= (5; 12) e v= ( -15; 8)
600
700
35,50
460
84,50
Para uma distribuição infinita de cargas que produz um campo de 4, 5 × 104 N/C a uma distância de 200 cm. Calcule a densidade de carga linear. Considere a constante eletrostática igual a 9.109 N.m2/c2.
5.10-6 C/m
3.10-9 C/m
7.10-9 C/m
3.10-7 C/m
9.10-9 C/m
Uma partícula de 1,8 nC está no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Qual é aproximadamente o fluxo elétrico em N/C .m2 através da superfície? Considere a permissividade elétrica igual a 8,85 x 10 -12 farad por metro.
92
652
203
402
562
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 5 x 105 N m²/C
ΦE = 4 x 106 N m²/C
A figura abaixo representa três esferas puntiformes fixas, no vácuo.calcule aproximadamente a intensidade da força elétrica resultante sobre a esfera Q2 , considere a constante eletrostática igual a  N.m²/c².
N.m²/c².
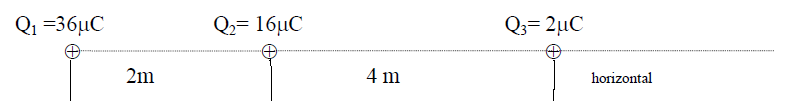
600
700
35,50
460
84,50
Para uma distribuição infinita de cargas que produz um campo de 4, 5 × 104 N/C a uma distância de 200 cm. Calcule a densidade de carga linear. Considere a constante eletrostática igual a 9.109 N.m2/c2.
5.10-6 C/m
3.10-9 C/m
7.10-9 C/m
3.10-7 C/m
9.10-9 C/m
Uma partícula de 1,8 nC está no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Qual é aproximadamente o fluxo elétrico em N/C .m2 através da superfície? Considere a permissividade elétrica igual a 8,85 x 10 -12 farad por metro.
92
652
203
402
562
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 5 x 105 N m²/C
ΦE = 4 x 106 N m²/C
A figura abaixo representa três esferas puntiformes fixas, no vácuo.calcule aproximadamente a intensidade da força elétrica resultante sobre a esfera Q2 , considere a constante eletrostática igual a  N.m²/c².
N.m²/c².
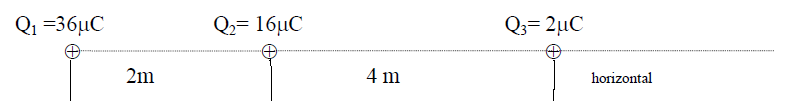
5.10-6 C/m
3.10-9 C/m
7.10-9 C/m
3.10-7 C/m
9.10-9 C/m
Uma partícula de 1,8 nC está no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Qual é aproximadamente o fluxo elétrico em N/C .m2 através da superfície? Considere a permissividade elétrica igual a 8,85 x 10 -12 farad por metro.
92
652
203
402
562
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 5 x 105 N m²/C
ΦE = 4 x 106 N m²/C
A figura abaixo representa três esferas puntiformes fixas, no vácuo.calcule aproximadamente a intensidade da força elétrica resultante sobre a esfera Q2 , considere a constante eletrostática igual a  N.m²/c².
N.m²/c².
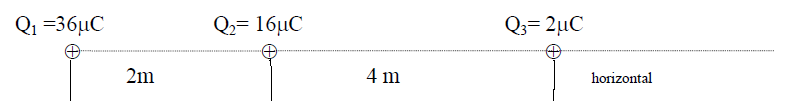
92
652
203
402
562
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 5 x 105 N m²/C
ΦE = 4 x 106 N m²/C
A figura abaixo representa três esferas puntiformes fixas, no vácuo.calcule aproximadamente a intensidade da força elétrica resultante sobre a esfera Q2 , considere a constante eletrostática igual a  N.m²/c².
N.m²/c².
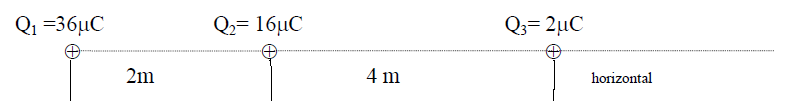
ΦE = 2 x 105 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 5 x 105 N m²/C
ΦE = 4 x 106 N m²/C
A figura abaixo representa três esferas puntiformes fixas, no vácuo.calcule aproximadamente a intensidade da força elétrica resultante sobre a esfera Q2 , considere a constante eletrostática igual a  N.m²/c².
N.m²/c².